Theory

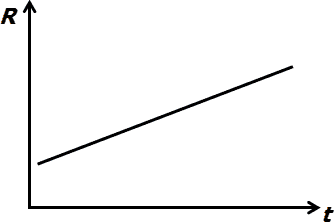
Electrical Resistance of Metals

In the case of metallic materials, the influence of structure and temperature is given by the Mathiessen rule that the resistivity can be divided into two components:

ρ = ρ_{S} + ρ_{T}

where ρ_S is a component that depends only on the structure and composition is related to the metal and its processing technology and does not depend on temperature. On the other hand, component ρ_T is a component that depends only on temperature. The alloy has a structural component usually more influential than the pure metals, alloys, because most shows less dependence on temperature change in resistance than pure metals.

With increasing temperature in the metal increases the amplitude of thermal motion of atoms, reduces the mean time between collisions of electrons with thermal lattice vibrations, and thus leads to the growth of resistivity with temperature. Since the range of measured temperatures, that $R = ρ \cdot \frac{ℓ}{S}$ , where L (the length of the conductor) and S (cross-sectional area) are constant, the increase in electrical resistance can be expressed using a simplified formula:

R = R_{0} \cdot [1 + α \cdot (t - t_{0})]

(1)

where R is the resistance at temperature t and R₀ is the resistance at temperature t₀. We can then express from relationship (1) formula to obtain the temperature coefficient of electrical resistance of α:

α = \frac{R - R_{0}}{R_{0} · (t - t_{0})}

(2)

t	[°C]	– temperature at the end of the measurement
t₀	[°C]	– temperature at the start of the measurement
R	[Ω]	– resistance at temperature t
R₀	[Ω]	– resistance at temperature t₀

The temperature coefficient of resistivity α observed at t₀ = 20 °C is shown in the school tables.

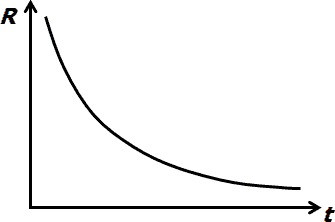
Electrical Resistance of Semiconductors

The semiconductor materials, like metal for the temperature dependence of resistance on temperature. Unlike metals, but the principle is the conductivity of different semiconductors. At absolute zero temperature, all electrons are tightly bound to their nuclei and the material cannot conduct current. Electrons must have some energy to "jump" over the so-called band gap into the conduction band and can participate in the current conduction. As the temperature increases, the concentration of charge carriers increases and the electrical resistance of the material decreases. While this phenomenon by trying to suppress conventional semiconductor devices, thermistors on him trying to contrast the composition of appropriate technology and highlight.

NTC thermistors, as representatives of the semiconductor components are negative temperature coefficient of resistance (when the component heats up, the resistance decreases) and preparation of semiconducting materials, usually based on oxides of nickel, manganese, cobalt, iron and titanium. For the temperature dependence of resistance of NTC thermistor is used in engineering practice the expression:

R = R_{0} · e^{- β \cdot (\frac{1}{T_{0}} - \frac{1}{T})}

(3)

T	[K]	– thermodynamic temperature measurement at the end
T₀	[K]	– thermodynamic temperature at the start of the measurement
R	[Ω]	– resistance of the thermodynamic temperature T
R₀	[Ω]	– resistance of the thermodynamic temperature T₀
β	[K]	– so-called thermistor temperature constant

The thermistor temperature constant β is related to the activation energy ΔE of the charge carriers, which is significantly affected by the composition and preparation technology of the semiconductor thermistor. To calculate the coefficient β, we use the measured resistance values of the thermistor: