Zvolte jazyk
V případě kovových materiálů je vliv struktury a teploty dán Mathiessenovým pravidlem, podle něhož můžeme rezistivitu rozdělit na dvě složky:
ρ = ρS + ρT
kde ρS je složka závislá pouze na struktuře a souvisí se složením kovu, jeho zpracováním a technologii a nezávisí na teplotě. Naopak složka ρT je složka závislá pouze na teplotě. U slitin má strukturní složka zpravidla větší vliv než u čistých kovů, proto většina slitin vykazuje menší závislost změny odporu na teplotě než čisté kovy.
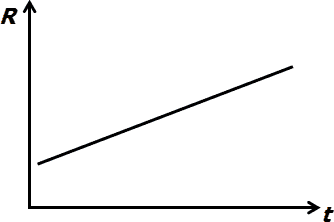
S rostoucí teplotou se v kovech zvětšuje amplituda tepelného pohybu atomů, zkracuje střední doba mezi srážkami elektronů s tepelnými kmity mřížky, a tím dochází k růstu měrného odporu s teplotou. Jelikož v rozsahu měřených teplot platí že R = ρ.L/S, kde délka vodiče L i plocha průřezu S jsou konstantní, můžeme růst elektrického odporu vyjádřit zjednodušeným vztahem:
R = R0 . [1 + α.(t – t0)]
(1)
kde R je odpor při teplotě t a R0 je odpor při teplotě t0. Ze vztahu (1) pak můžeme vyjádřit výraz pro získání teplotního součinitele elektrického odporu α:
| α = | R – R0 |
| R0 . (t – t0) |
(2)
| t | [°C] | – teplota na konci měření |
| t0 | [°C] | – teplota na počátku měření |
| R | [Ω] | – odpor při teplotě t |
| R0 | [Ω] | – odpor při teplotě t0 |
V tabulkách je uváděn teplotní součinitel měrného odporu α zjištěný při teplotě t0 = 20 °C.
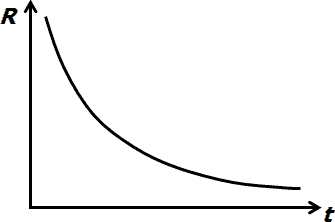
U polovodičových materiálů se podobně jako u kovových využívá teplotní závislosti odporu na teplotě. Na rozdíl od kovů je ale princip vodivosti polovodičů odlišný. Při teplotě absolutní nuly jsou všechny elektrony pevně vázány ke svým jádrům a materiál nemůže vést proud. Elektronům je třeba dodat určitou energii k tomu, aby „přeskočily“ přes tzv. zakázaný pás do pásu vodivostního a mohly se účastnit vedení proudu. S rostoucí teplotou tedy bude koncentrace nosičů náboje růst a elektrický odpor materiálu se bude snižovat. Zatímco se tento jev snažíme u klasických polovodičových součástek potlačit, u termistorů se ho naopak snažíme vhodnou technologií a složením zvýraznit.
NTC termistory, jako reprezentanti polovodičů, jsou součástky se záporným teplotním součinitelem odporu (při zahřátí součástky odpor klesá) a připravují se z polovodivých materiálů, nejčastěji na bázi oxidů niklu, manganu, kobaltu, železa a titanu. Pro teplotní závislost odporu NTC termistoru se užívá v technické praxi výrazu:
| R = R0·e | [–β·( | 1 | – | 1 | )] |
| T0 | T |
(3)
| T | [K] | – termodynamická teplota na konci měření |
| T0 | [K] | – termodynamická teplota na počátku měření |
| R | [Ω] | – odpor při termodynamické teplotě T |
| R0 | [Ω] | – odpor při termodynamické teplotě T0 |
| β | [K] | – tzv. teplotní konstanta termistoru |
Teplotní konstanta termistoru β souvisí s aktivační energií nosičů náboje ΔE, která je významně ovlivněna složením polovodiče a technologií přípravy termistoru. Pro výpočet koeficientu β můžeme použít naměřené hodnoty odporů termistoru:
| β = | ln( | R | ) |
| R0 | |||
| 1 | – | 1 | |
| T | T0 | ||
(4)
Vztah mezi aktivační energií ΔE a vypočítaným součinitelem β se dá s dostatečnou přesností vyjádřit jako:
ΔE = β.k
(5)
(Boltzmannova konstanta k = 1,38.10–23 J·K–1)
 |
This Web is translated into English
by Google Translate |