Popis aparatury - Určení zemského magnetismu

Aparatura

Fyzikální princip měření

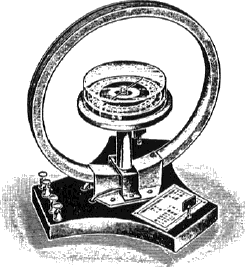
Obr. 1 - tangentová buzola
zdroj: http://vnuf.cz/sbornik/prispevky/ soubory/04_21/image002.jpg

Klasickou metodou měření velikosti horizontální složky ${\vec{B}}_{H}$ zemského magnetického pole je metoda tangentové buzoly. Je to přístroj (obr. 1), který se skládá z kruhové cívky o větším středním průměru a obsahující malý počet závitů uspořádaných do úzkého svazku. Ve středu cívky je malá magnetka, která se otáčí kolem svislé osy.

Před měřením postavíme cívku tak, aby její rovina souhlasila s rovinou magnetického poledníku a tím i se směrem magnetky. Začne-li pak cívkou protékat proud I, vzniká v místě magnetky magnetické pole, jehož magnetická indukce ${\vec{B}}_{C}$ je dána vektorovým součtem magnetického pole Země ${\vec{B}}_{H}$ a magnetickým polem vytvořeným cívkou $\vec{B}$ (viz obr. 2).

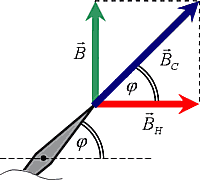
Obr. 2 - skládání vektorů magnetické indukce

Vlivem pole cívky, jehož vektor $\vec{B}$ stojí kolmo na horizontální složku ${\vec{B}}_{H}$ zemského magnetického pole, se magnetka vychýlí ze své původní polohy o určitý úhel φ a zaujme novou rovnovážnou polohu odpovídající směru magnetické indukce ${\vec{B}}_{C}$ výsledného pole (obr. 2). Po dosazení vzorce pro velikost vektoru $\vec{B}$ do platného vztahu:

tg φ = \frac{| \vec{B} |}{| {\vec{B}}_{H} |} = \frac{B}{B_{H}}

(1)

získáme výsledný vztah pro zemský magnetismus v závislosti na napájecím proudu cívky (lze změřit ampérmetrem) a výchylkou buzoly (lze odečíst na buzole).

Měřicí aparatura

Ve školní praxi zpravidla již nemáme ve sbírkách tangentovou busolu, můžeme tedy při měření B_H improvizovat. K improvizaci lze použít jednoduchý solenoid navinutý z měděného drátu na obal plastové láhve, do které lepenkou upevníme turistickou buzolu (viz obrázek vpravo). Za vztah mezi elektrickým proudem a magnetickou indukcí cívky pak dosazujeme klasický vztah pro solenoid.

V naší laboratoři jsme je však pro tento experiment připravili trochu sofistikovanější konstrukci. Spojili jsme hned několik zkušeností s tímto pokusem a navrhli jsme následující sestavu. Princip pokusu je stále stejný, jen místo jednoduché kruhové cívky jsme použili speciální dvojici cívek, která díky své konfiguraci tvoří tzv. Helmholtzovy cívky^*). Použitím Helmholtzových cívek jsme nejen získali lepší přístup k buzole a tedy i její čitelnost, ale především homogennější magnetické pole cívek. V neposlední řadě jsme chtěli, aby se studenti střední školy setkali s těmito cívkami, které se v praxi často používají a přesto se o nich při hodinách fyziky příliš nehovoří. Rozšiřující bude i následné uvedení vztahu pro magnetické pole ve středu Helmholtzových cívek.

^*)

Pár Helmholtzových cívek se skládá ze dvou identických kruhových magnetických cívek, které jsou umístěny symetricky na každé straně experimentální plochy podél společné osy a jsou od sebe ve vzdálenosti rovnající se jejich poloměru. Proud oběma cívkami je stejný a směr souhlasný. Výsledné pole mezi cívkami je téměř homogenní.

Měření - platné vztahy

Vyjdeme z již zmíněného vztahu (1), kde B je magnetická indukce cívek, která vychyluje střelku buzoly o úhel φ ze směru místního magnetického poledníku tj. směru horizontální složka magnetického pole Země B_H.

Dosazením výrazu pro magnetickou indukci Helmholtzových cívek:

B = {(\frac{4}{5})}^{\frac{3}{2}} \cdot μ_{0} \cdot \frac{N \cdot I}{r}

(2)

dostaneme výsledný vztah:

B_{H} = {(\frac{4}{5})}^{\frac{3}{2}} \cdot μ_{0} \cdot \frac{N \cdot I}{r} \cdot \frac{1}{tg φ}

(3)

kde:
N		- počet závitů každé z cívek; N = 240
r	[m]	- poloměr cívek (též vzájemná vzdálenost cívek); r = 15 cm
I	[A]	- elektrický proud v cívkách;
φ	[°]	- odchylka magnetické střelky odpovídající proudu I;
μ₀	[T·m/A]	- permeabilita vakua (vzduchu); μ₀ = 4π ·10^–7 T·m/A

Stačí tedy naměřit několik hodnot budicího elektrického proudu cívek I a příslušných odchylek φ. Hledanou hodnotu horizontální složky magnetické indukce Země B_H lze pak určit jako aritmetický průměr dílcích výsledků.

Zpracování pomocí tabulkového kalkulátoru (bez určení hodnoty B):

Uvědomíme-li si, že získaný vztah (3) lze upravit do podoby:

B_{H} = \underset{┖━ konst. K ━┚}{{(\frac{4}{5})}^{\frac{3}{2}} \cdot \frac{μ_{0} \cdot N}{r}} \cdot \frac{I}{tg φ}

tg φ = \frac{K}{B_{H}} \cdot I

(4)

což ukazuje, že vztah mezi hodnotou funkce tg φ a proudem I je lineární (dokonce přímá úměrnost!). Provedeme-li dostatek měření pro různé úhly výchylky magnetické střelky a odpovídající elektrické proudy cívkami, můžeme hodnoty funkce tg φ a proudů I vložit do grafu. Pohled na tvar grafu nás přesvědčí o tom, zda byly naše úvahu o vzájemné závislosti pravdivé. Pokud by závislost nebyla lineární znamená to, měření může být zatíženo nějakou systematickou chybou - např. špatně se otáčející střelka v buzole apod.

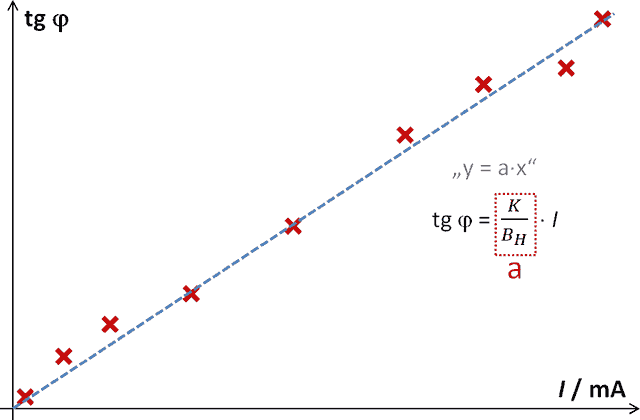
Graf č. 1 – Závislost hodnoty funkce tangens úhlu výchylky magnetické střelky na budícím proudu Helmholtzových cívek

Pomocí tabulkového kalkulátoru (MS Excel, OO Calc apod.) lze získat pomocí lineární regrese hodnotu směrnice a – viz graf 1 a výraz (4). Tato hodnota je podílem konstantního výrazu K a hledané hodnoty horizontální složky zemského magnetismu B_H. Po vydělení konstantního výrazu K číselnou hodnotou směrnice a dostáváme lokálně platnou hodnotu horizontální složky magnetické indukce Země.

Video tutorial

PRO ZOBRAZENÍ VÝKLADU A VYSVĚTLIVEK ZAPNĚTE VE VIDEU TITULKY!

Remote-LAB GymKT

Vzdálená internetová laboratoř

Reálné fyzikální pokusy ovládané přes Internet

Určení horizontální složky mag. pole Země