Teorie
- POZNÁMKA:
- Odvození výrazů pro difrakční maxima (popř. minima) na štěrbině, dvojštěrbině a mřížce jsou zde uvedena na středoškolské úrovni. Kdo se chce dozvědět o odvození těchto vzorců více a podívat se na „korektní“ odvození vzorců, může si nastudovat následující materiál: Studium difrakčních jevů – TEORIE – doplněk .
Difrakce světla
Ohyb světla (nebo-li difrakci) pozoroval a popsal již okolo roku 1660 italský učitel matematiky Francesco Maria Grimaldi. Ten v zatemněné místnosti nechal dopadat sluneční světlo na malý otvor a do dráhy vzniklého světla umisťoval různé předměty a studoval jejich stín. Tím zjistil, že stíny jsou neostré a že jsou navíc ohraničené barevnými proužky.
Základní předpoklad paprskové optiky, že se světlo šíří přímočaře podle zákona přímočarého šíření, platí totiž jen omezeně. Ve skutečnosti je šíření světla, podobně jako každého vlnění (např. šíření zvukového vlnění), ovlivněno jeho vlnovými vlastnostmi. Poznáme to právě na překážkách, které jsou srovnatelné s jeho vlnovou délkou. V takovém případě na překážce dochází k ohybu světla – tzv. difrakci. Tento je se projevuje tak, že se světlo šíří částečně i do prostoru za překážkou, kam by se podle paprskové optiky nikdy šířit nemělo, tzn. světlo se šíří i do oblasti geometrického stínu. Hranice mezi světlem a stínem potom není ostrá a na stínítku za překážkou se vytváří tzv. ohybový (též difrakční) obrazec.
Rozdělení ohybových jevů
Ohybové jevy se zpravidla rozdělují na dva základní druhy:
Pokud světlo dopadá na překážku z bodového zdroje v konečné vzdálenosti od překážky, jde o jevy Fresnelovy [frenelovy].
Je-li zdroj (a detektční stínítko) v nekonečnu, potom jsou vlny přicházející od zdroje rovinné a fáze kmitů je stejná ve všech bodech překážky (předpokladu, že vlnění dopadá kolmo na překážku). Podmínky nekonečně vzdáleného zdroje (popř. stínítka) se v praxi dosahuje užitím čoček umístěných před a za překážkou. V tomto případě jde o jevy Fraunhoferovy. Fraunhofer umísťoval ohybovou překážku do blízkosti objektivu, kterým zobrazoval bodový nebo štěrbinový zdroj světla a studoval ohybové jevy v rovině geometrického obrazu. Rozkladem světla pomocí optické mřížky položil základy mřížkové spektroskopie.
Nadále se budeme zabývat jen Fraunhoferovu difrakcí.
Ohyb světla na štěrbině
Předpokládejme, že rovinná světelná vlnoplocha o vlnové délce λ dopadá na štěrbinu šířky a. Každý bod štěrbiny se podle Huygensova principu stává zdrojem elementárního vlnění, které se z něho šíří v elementárních vlnoplochách i do prostoru za překážkou. Do každého bodu na stínítku pak dopadá světlo z každého bodu štěrbiny. Protože byla štěrbina osvětlena rovinou monochromatickou vlnou, můžeme tato elementární vlnění považovat za koherentní a na stínítku vznikne ohybový obrazec (viz obr. 1).
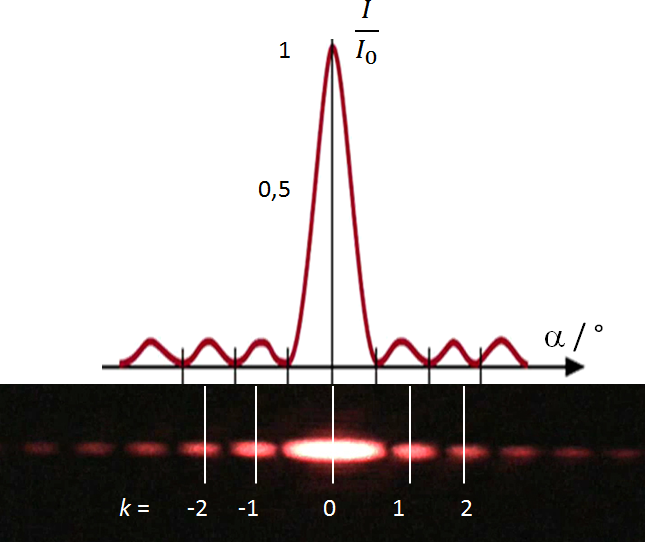
Obr. 1 – Intenzita světla v ohybovém obrazci na štěrbině
(nahoře: graf průběhu intenzity; dole: reálný obrazec)
Rovinná vlnoplocha dopadá na štěrbinu, na které dochází k ohybu vlnění. Na detekčním stínítku mají vlny svazku různou fázi v závislosti na dráze, kterou do daného místa urazily. Vzájemným skládáním těchto paprsků koherentního vlnění vzniká zmíněný difrakční obrazec.
Nyní si odvodíme podmínku pro vznik interferenčních minim difrakčního obrazce na štěrbině. Rovinná vlna o vlnové délce λ dopadá kolmo na štěrbinu o šířce a. Do daného místa dopadají paprsky z celého prostoru štěrbiny. Pro názornost jsou v obrázku vyznačeny jen paprsky vycházející z okrajů štěrbiny (body A a B). Intenzita světla v místě P (vzdáleného y od osy štěrbiny) je znázorněna červenou křivkou. Situaci ilustruje obrázek 2.
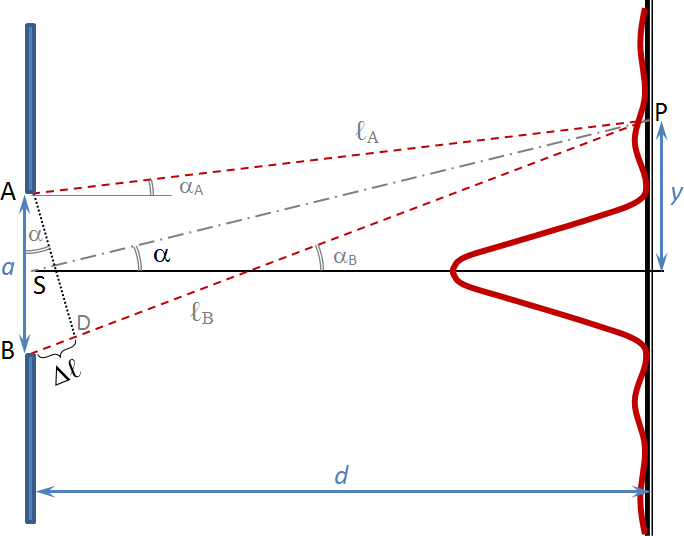
Obr. 2 – odvození interferenční podmínky minima na štěrbině.
Dráhový rozdíl mezi vlnou, která se šíří z bodu A (horní krajní bod štěrbiny) a vlnou, která se šíří z bodu B (dolní okraj štěrbiny) je Δℓ (vyznačeno v obr. 2; viz pozn. 1). Dráhový rozdíl mezi vlnou, která se šíří ze středu štěrbiny S a vlnou, která se šíří z bodu A, tak díky podobnosti trojúhelníků činí Δℓ/2. Díky osové symetrii svazku paprsků mířících z celé plochy štěrbiny do bodu P (osa v obrázku vyznačena čerchovaně) lze najít ke každému paprsku šířícímu se z libovolného bodu mezi body A a S paprsek šířící se z bodů mezi body B a S, který je dráhově opožděn o Δℓ/2. Podmínka interferenčního minima říká, že všechny vlny se vzájemně vyruší, bude-li tento dráhový rozdíl Δℓ/2 roven lichému násobku půlvln. Upravíme-li tuto podmínku pro celý dráhový rozdíl Δℓ musí tedy platit, že je roven sudému násobku půlvln (dvojnásobek lichého násobku je sudé číslo).
Pro zjednodušení výpočtu dráhového rozdílu vln ℓA a ℓB jsme předpokládali, že vzdálenost stínítka d je mnohem větší než šířka štěrbiny a. Potom jsou úhly αA a αB přibližně stejně velké (ozn. α) a směry obou vln je možné považovat za rovnoběžné a dráhový rozdíl drah ℓA a ℓB bude dán vzdáleností Δℓ. (v obrázku díky nesplnění podmínky a << d to tak pochopitelně nevypadá).
Z obrázku 2 též vidíme, že dráhový rozdíl vln Δℓ si můžeme vyjádřit z pravoúhlého trojúhelníku ABD, jehož přeponou je šířka štěrbiny a, dráhový rozdíl Δℓ je podvěsnou protilehlou k úhlu α.
Pro dráhový rozdíl tedy z geometrie plyne:
Z vlnové optiky (resp. z výše odvozené úvahy) víme, že dráhový rozdíl pro podmínku minima musí být roven dvojnásobku lichých násobků poloviny vlnové délky.
Podmínku pro polohu ohybových minim tedy zapíšeme:
což lze upravit do podoby:
| kde: |
a |
[m] |
– šířka štěrbiny |
| λ |
[m] |
– vlnová délka |
| α |
[°; rad] |
– úhel (směr), pro který nastává dané minimum |
| k |
|
– celé číslo kromě nuly
(pro k = 0 nastává hlavní ohybové maximum!) – čti Pozn. 2 |
Maxima potom nastávají mezi danými minimy – v obrázku 1 vyznačeny bíle i s danými hodnotami čísla k (tzv. řády maxima).
V některých textech věnovaným difrakci na štěrbině je na základě chybného odvození dráhového rozdílu paprsků z bodů A a B prezentován vztah (1) jako podmínka pro difrakční maxima. To ale není pravda! Asi je to způsobeno podobným způsobem odvození (a i podobností vztahu) pro podmínku maxima na difrakční mřížce. Platnost chybného závěru, že vztah (1) je podmínkou maxima, je v některých textech chybně dokládána ukázkou toho, že vztah správně určuje maximum nultého řádu. To je sice pravda, ale nultý řád je bohužel jediné maximum, které v tomto případě vztah určuje správně! Podmínka (1) je skutečně (a je to experimentálně podložené) podmínkou pro minima prvního a vyššího řádu (k = 1, 2, …). Dosazení hodnoty k = 0 je fyzikální nesmysl, protože žádné nulté minim v difrakčním obrazci neexistuje!
Ohyb světla na více štěrbinách
Nejvýraznější ohybové obrazce vznikají, pokud světlo necháme dopadat na více úzkých štěrbin. Soustavu velkého počtu štěrbin nazýváme optická mřížka (viz dále). Parametry soustavy štěrbin jsou šířka štěrbiny a a vzdálenost středů sousedních štěrbin b – u mřížky nazývaná mřížková konstanta (popř. perioda mřížky).
Pro odvození podmínky interferenční maximum na mřížce, si nejdříve odvodíme vztah pro ohyb světla na soustavě dvou štěrbin (tzv. dvojštěrbina).
Ohyb na dvojštěrbině
Na dvě štěrbiny necháme dopadat ze vzdáleného zdroje monofrekvenční světlo. Opět budeme předpokládat, že šířka štěrbiny a a vzdálenost středů sousedních štěrbin b je mnohem menší, než je vzdálenost stínítka d od dvojice štěrbin. Při dopadu rovinné vlny nastanou dva jevy – difrakce na každé štěrbině (viz dříve) a pak též interference dvou koherentních vln ze dvou štěrbin.
Za štěrbinami se světlo šíří opět všemi směry. Stejným způsobem jako na jedné štěrbině vezmeme v úvahu paprsky, které se od původního směru odklonily o úhel α, dopadají do bodu P a vycházejí z odpovídajících si bodů – jak je naznačeno na obrázku 3. Odpovídající si body jsou horní okraje první a druhé štěrbiny (jejich vzájemná vzdálenost je b).
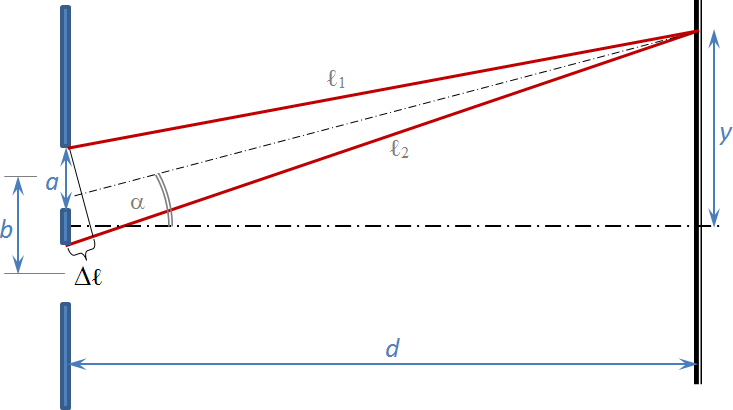
Obr. 3 – odvození interferenčního maxima na dvojštěrbině
Z obrázku potom pro dráhový rozdíl těchto paprsků ℓ1 a ℓ2 vyplývá:
| kde: |
Δℓ |
[m] |
– dráhový rozdíl |
| b |
[m] |
– vzájemná vzdálenost štěrbin |
| α |
[°; rad] |
– odchylka vlny od původního směru rovinné vlny |
Ve směrech, kde bude dráhový rozdíl vln roven sudému násobku půlvln, dojde k zesílení.
Podmínka interferenčního maxima v případě dvojštěrbiny je:
| kde: |
b |
[m] |
– vzájemná vzdálenost štěrbin |
| λ |
[m] |
– vlnová délka použitého světla |
| α |
[°; rad] |
– úhel (směr), pro který nastává maximum |
| k |
|
– celé číslo (tzv. řád maxima) |
Ve směrech, pro které je dráhový rozdíl roven lichému násobku půlvln, nastává interferenční minimum.
Výsledný ohybový obrazec na dvojštěrbině ještě ovlivní, jak bylo zmíněno, i difrakce na štěrbinách samotných. Výsledný obrazec tedy vytvoří složení širší maxima a minima, která odpovídají ohybu na jedné štěrbině (obalová křivka) a řada světlých a tmavých proužků, které jsou výsledkem interference světelného vlnění ze dvou štěrbin („promodulování“ obrazce – viz obr. 4; pravá část). Lze tedy říci, že úzké ekvidistantní proužky jsou výsledek interference z jednotlivých štěrbin, zatímco široké oblasti světla a tmy jsou důsledek difrakce na šířce štěrbiny.
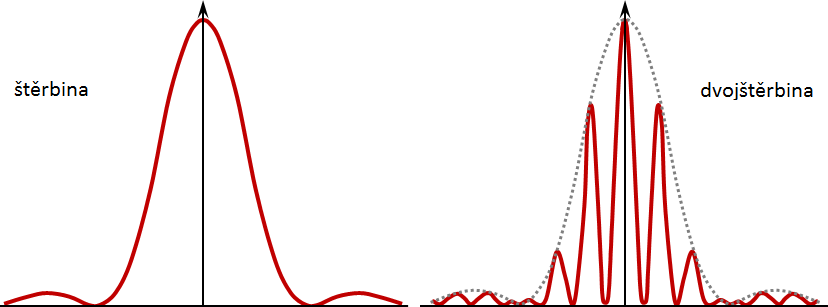
Obr. 4 – srovnání difrakčního obrazce pro jednu štěrbinu (vlevo) a dvojici stejně širokých štěrbin (vpravo)
Ohyb světla na mřížce
Mřížku si můžeme představit jako soustavu složenou z velkého počtu štěrbin umístěných navzájem ve stejných vzdálenostech b. Každý z bodů štěrbin je opět možné považovat za bodový zdroj světla, z něhož se světlo šíří podle Huygensova principu. Z analogie s dvojštěrbinou (viz dříve) potom pro dráhový rozdíl odpovídajících si bodů štěrbin mřížky vyplývá stejný vztah pro interferenční maximum jako u dvojštěrbiny. Následující obrázek ilustruje, charakter difrakčního obrazce pro různý počet stejných štěrbin. Všimněte si, že pro dvě a více štěrbin se polohy maxim (popř. minim) nemění, jen se rozšiřuje oblast minim a naopak zužuje šířka maxim („zaostřování“ maxim).

Obr. 5 – srovnání difrakčních obrazců pro různé počty štěrbin (1, 2, 3 … 7) a mřížky
Podmínka pro interferenční maximum na mřížce odpovídá podmínce pro dvojštěrbiny, jen v případě mřížky jsou maxima „ostřejší“ (viz obr. 5):
| kde opět: |
b |
[m] |
– mřížková konstanta |
| λ |
[m] |
– vlnová délka použitého světla |
| α |
[°; rad] |
– úhel (směr), pro který nastává maximum |
| k |
|
– celé číslo (řád maxima) |










