Remote-LAB GymKT

Theory

Atomic nucleus

The atomic nuclei of matter commonly found in nature consist of protons and neutrons. They have a positive charge and almost all the mass of the atoms is concentrated in them (electrons are about 2000 times less massive than protons and neutrons). The number of protons in the nucleus is denoted by the proton number Z (related to the charge of the nucleus), the number of neutrons by the neutron number N, and the total number of nucleons (protons and neutrons) is given by the nucleon number A (A = Z + N, related to the mass of the nucleus). Based on the number of protons and neutrons in the nucleus, we introduce the terms nuclide, isotope and isobar.

Nuclide – represents a collection of identical atoms, whose nuclei have the same composition. This is expressed by the notation ${}_Z{}^{A}X^N$, where X represents the chemical symbol, e.g. ${}_{92}{}^{238}\text{U}^{146}$. Since the number of protons in the nucleus is given by the chemical symbol, we often write ${}^{A}X$ for short, so for example the notation ²³²Th gives Z = 90 (the order of thorium in the periodic table of elements) and N = 232 – 90 = 142.

Isotopes – are nuclides that have the same proton but different nucleon (and therefore neutron) numbers. So, for example, we say that ${}_6{}^{12}\text{C}^6$, ${}_6{}^{13}\text{C}^7$ and ${}_6{}^{14}\text{C}^8$ are different isotopes of carbon.

Isobars – are nuclides that have the same nucleon number but different proton numbers, e.g. ${}_{18}{}^{40}\text{Ar}^{22}$, ${}_{19}{}^{40}\text{K}^{21}$ and ${}_{20}{}^{40}\text{Ar}^{20}$.

Protons and neutrons reside in the atomic nucleus in a very small volume, so the protons are strongly repelled from each other by the electrostatic (Coulomb) force. The stability of the nucleus is provided by the nuclear force, which has a very short range (10^–15 m) and is much stronger than the electrostatic force. The essence of this force lies in the exchange of virtual particles called gluons.

Radioactivity

Of the more than 2,000 known nuclides, only 266 are stable. The others, whether found in nature or produced by nuclear reactions, are more or less rapidly spontaneously converted into other nuclides – they are radioactive.

By radioactivity we mean the ability of some atomic nuclei to emit radiation. In doing so, such a nucleus may change into another or at least lose some of its energy. In nuclear transformation, the structure of the nucleus changes, an isotope of one element changes into an isotope of another element. It has been empirically established that nuclei are stable, i.e. they do not undergo radioactive transformations, only at a certain ^N/_Z ratio. For stable light nuclei (Z ≤ 20) this ratio is equal to one (the exceptions are nuclei ${}_1{}^1\text{H}^0$ a ${}_2{}^3\text{He}^1$), for more massive nuclei it increases further up to a value of 1.52 for the heaviest stable nuclide ${}_{83}{}^{209}\text{Bi}^{126}$. If the composition of the nucleus deviates from the optimal ratio between protons and neutrons, it becomes radioactive. Some elements have only one stable isotope, while for others there are two or more stable isotopes.

There are three groups of radioactive transformations:

1. transformations in which Z changes at constant A (β^– and β⁺ transformations, electron capture)

2. transformations in which both Z and A change simultaneously (α transformation, nucleon emission, emission of heavier nuclei, spontaneous fission)

3. conversions caused by deexcitation of the nucleus in which only the energy content of the nucleus changes (γ-ray emission, internal conversion).

Mechanism of ionizing radiation energy loss

The radiation emitted by radioactive nuclides is a stream of material particles and photons. Their energy lies in the order of keV to MeV, which are several orders of magnitude higher than the ionisation energy of atoms and molecules. For this reason, it causes intense ionisation (hence the name ionising radiation) as it passes through matter. In addition to ionisation, atoms and molecules are also excited. The electrons released during ionisation have such energy that they themselves cause secondary ionisation and excitation.

The energy of the ionizing particle is reduced by the corresponding value of the ionization or excitation energy at each individual ionization or excitation . Since this energy represents only a small fraction of the energy of the particle, a large number of ions, free electrons and excited states are produced along the path of the ionising particle. Thus the particle gives up its energy to the substance until it gradually loses its ability to ionize and excite and is absorbed by the environment. If the layer of matter is thick enough, all the particles give up all their energy to the matter and the radiation is completely absorbed. The thickness of the layer that completely absorbs the radiation is referred to as the range of the radiation.

In our experiment we will investigate the absorption of β radiation (radioactive emitter:  ⁹⁰Sr), so we are concerned only with its absorption mechanism.

Mechanism of β-radiation absorption: ¹⁾

The linear energy transfer of β radiation is generally smaller than that of α radiation, for example. This is due to the smaller charge size of the electron compared to that of the helium nucleus and the fact that at a given energy the electron velocity is significantly higher. For this reason, β radiation has a greater penetration and range in the environment.

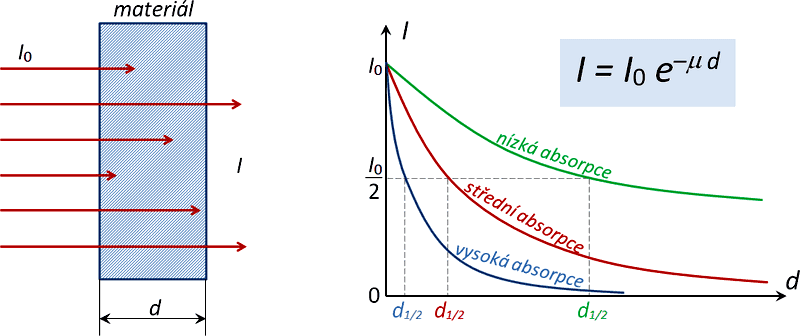
Fig. 1 – Basic laws of absorption of ionizing radiation in a substance of density ρ, proton number Z and thickness d.

The range is a few meters in gases (depending on the energy of the radiation), low energy β radiation is similar to α radiation in short range. The absorption curve of β radiation has an exponential waveform, which is described by an empirical relationship for the intensity of the radiation: ²⁾

where I₀ is the initial radiation intensity, d is the thickness of the absorbing layer and μ is the linear absorption coefficient (or linear attenuation coefficient). The latter depends on the electron density of the medium and the energy of the radiation. Its value depends on the density and proton number of the absorbing material and also significantly on the energy of the radiation. We can write for it:

where ρ is the density of the medium and the constant μ_m, which is already independent of the density, is called the mass absorption coefficient (also mass attenuation coefficient) for a given radiation type and corresponding energy spectrum. Furthermore, especially for technical purposes – such as shielding design, for example – instead of a linear attenuation coefficient, the tables give the value of the so-called half-layer (half-thickness) absorption $d_{\frac{1}{2}}=\frac{ln2}{\mu }$, which is the thickness of the layer of a given material that will attenuate the intensity of the radiation in question by half.

₁₎

The absorption of β radiation is also contributed to a lesser extent by the formation of braking (X-ray) and so-called Cherenkov radiation.

₂₎

The basic property of an exponential function with a negative exponent is that it approaches zero only in the limit at infinity. This would mean that radiation can virtually never be completely removed. However, this is only theoretically the case. In reality, each emitter emits only a finite number of particles. In practice, after passing through a sufficient thickness (tens or hundreds of d_1/2), the last particle is always eventually absorbed.