Teorie
Mechanické kmitání
Mechanické kmity jsou speciálním případem obecného mechanického pohybu hmotného bodu, při kterém se tento bod pohybuje v omezené oblasti kolem rovnovážné polohy. Rovnovážná poloha je místo stabilní rovnováhy, ve které na hmotný bod nepůsobí žádná výsledná síla. Do rovnovážné polohy klademe pokud možno počátek soustavy souřadnic. Potom polohový vektor hmotného bodu je současně jeho výchylkou z rovnovážné polohy.
Opakují-li se kmity pravidelně, tj. opakují-li se všechny fyzikální veličiny charakterizující kmitavý pohyb (poloha, rychlost, zrychlení), jedná se o periodické a pokud je časový průběh popsatelný funkcí sinus (resp. cosinus), říkáme také harmonické kmity. Soustava, která mechanické kmity koná, se nazývá oscilátor.
Kmity podle působící síly
Příčinou každého pohybu je síla. Příčinou kmitavého pohybu je tzv. direktivní (elastická) síla. Bez této síly mechanické kmity nevzniknou.
Podle působení sil dělíme kmitání na základní případy:
Působí-li jen direktivní síla, vzniknou vlastní kmity. (Amplituda vlastních kmitů je konstantní, vlastní kmity jsou přesně periodicky.)
Působí-li kromě direktivní síly ještě tlumící síla (Tlumící silou může být tření, odpor prostředí apod.) a již žádná jiná, vzniknou tlumené kmity. Tlumené kmity jsou téměř periodické - tzv. kvaziperiodické (Amplituda klesá s časem).
Působí-li kromě direktivní a tlumící síly ještě vnější budící síla, vzniknou nucené kmity. (Amplituda oscilátoru závisí na frekvenci vlastních kmitů a budící frekvenci.)
Vlastní kmity
V případě pružinového oscilátoru je direktivní síla dána „pružností“ použité pružiny. Tato síla je přímo úměrná prodloužení pružiny, tedy výchylce oscilátoru. Směr síly je však opačný než je směr výchylky - Pružina působí proti výchylce (snaží se vrátit do rovnovážné polohy).
To lze zapsat výrazem:
ve kterém je F – (direktivní) síla, y – výchylka oscilátoru a k – tzv. tuhost pružiny (konstanta popisující „pružnost“ pružiny).
Dosazením výrazu (1) do 2. Newtonova zákona (F = m·a) získáme pohybovou rovnici (diferenciální rovnice). Jejím dořešením získáme závislost okamžíté výchylky y na čase t, která má dle obecného tvaru pro harmonický pohyb:
| kde: |
ym – maximální výchylka (amplituda) |
| ω – úhlová rychlost kmitání |
| φ0 – počáteční fáze kmitání |
následující podobu:
| y(t) = ym· sin( |
|
· t + φ0) |
Ze vztahu (2) tedy získáváme výraz pro úhlovou frekvenci vlastních kmitů ω0, nebo ještě lépe výrazy pro periodu T a frekvenci vlastních kmitů f0:
Interaktivní HTML5 animace:
Tato HTML5-App zobrazuje závislost okamžité výchylky, rychlosti, zrychlení, síly a energie při oscilacích pružinového oscilátoru (vliv tření neuvažueme).
Tlačítko „Reset“ nastaví oscilátor do počáteční polohy. Druhým tlačítkem můžete simulaci spustit popřípadě pozastavit. Jestliže zvolíte volbu „Zpomaleně“, pohyb se desetkát zpomalí. V určitých mezích můžete měnit tuhost pružiny, velikost gravitačního zrychlení, hmotnost závaží a amplitudu oscilací (nezapoměňte po zadání stisknout „Enter“). Dále lze pomocí přepínačů volit zobrazování pěti základních fyzikálních veličin.
Tlumené kmity
U reálných oscilátorů se díky všeobecným ztrátám (např. odpor prostředí proti pohybu tělesa) zmenšuje celková energie oscilátoru. V důsledku toho se postupně zmenšuje i amplituda kmitů. V takovém případě hovoříme o tlumeném kmitání.
Soustavu vykonávající tlumené kmitání můžeme kromě dříve popsaných parametrů (ym, k a m) ještě charakterizovat veličinou δ – tzv. součinitel tlumení (jednotka s–1), která právě popisuje, jak moc je soustava „zatlumena“.
Právě podle stupně zatlumení můžeme rozlišit tři základní typy pohybu:
1. Podkritické tlumeni oscilátoru
Pokud je tlumení soustavy poměrně malé (tedy: je splněna podmínka δ < ω0), je tlumení takové, že vzniknou kvaziperiodicke kmity s výchylkou popsanou výrazem:
Všimněme si, že se oproti netlumenému oscilátoru změnila nejen amplituda (viz dále), ale též úhlová frekvence kmitů. Tuto úhlovou frekvenci podkriticky tlumených kmitů ωT získáme ze vzorce:
ωT = (ω02 – δ2)
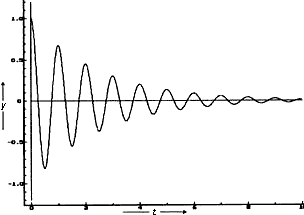
Z obrázku vpravo vidíme postupné zmenšování amplitudy tlumeného kmitání. V případě těchto podkriticky tlumených kmitů má amplituda exponenciálně klesající průběh, což vyjadřuje i výraz: ym·e–δt ve výrazu pro y(t).
2. Kritické tlumeni oscilátoru
Pokud je tlumení soustavy takové, že je splněna podmínka δ = ω, je tlumení oscilátoru kritické. Pak též platí, že ω02 – δ2 = 0 a tedy ωT = 0. To znamená, že periodicke ani kvaziperiodicke kmity nevzniknou.
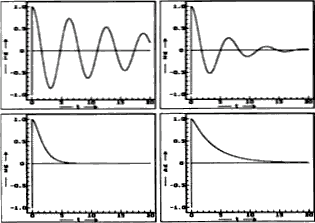
Na obrázku vpravo vidíme časové průběhy tlumeného kmitání pro různá tlumení. Horní dva grafy ukazují kvaziperiodické kmitání při podkritickém tlumení (Všimněte si různé „rychlosti útlumu“ při různých tlumení!), v dolní řádce pak případ kritického (levý) a nadkritického (pravý) tlumení. V obou případech (tj. kritického a nadkritického tlumení) již nelze mluvit o kmitání.
3. Nadkritické tlumeni oscilátoru
Podobně předešlému případu nevzniknou periodické ani kvaziperiodické kmity při velkém tlumení, tedy při splnění podmínky δ > ω0. Pak říkáme, že je tlumení oscilátoru nadkritické. V takovém případě je i výraz ω02 – δ2 < 0 a díky tomu úhlová frekvence ωT v reálné oblasti neexistuje.
Nucené (buzené) kmity
Zmenšováním amplitudy u podkriticky tlumených kmitů se též zmenšuje i celková energie oscilátoru a tedy za nějaký čas kmity zcela vymizí. Chceme-li, aby se kmity udržely, je nutné ztracenou energii pravidelně doplňovat prací nějaké vnější síly. To je případ buzeného harmonického oscilátoru. Vzniklé kmity nazveme buzené nebo také nucené. Na oscilátor nyní tedy musí působit, kromě direktivní a tlumící síly, ještě i periodická budící síla. Výsledná frekvence oscilátoru se po krátké době přizpůsobí frekvenci budící síly ωB, amplituda oscilátoru však, jak uvidime dále, bude záviset na frekvenci vlastních kmitů a budící frekvenci.
Výsledné buzené kmitání (po ustálení na budící frekvenci ωB) můžeme obecně popsat rovnicí:
kde amplituda výsledného kmitání yB závisí na úhlové frekvenci vlastního a buzeného kmitání (stejně tak na součiniteli tlumení) dle následujícího poměrně složitého vztahu:
| yB = |
FBm |
|
| m · (ω02 – ωB2)2 + (2 δ ωB)2 |
kde FBm je amplituda budící síly a m hmotnost závaží zavěšeného na pružině.
Rezonace
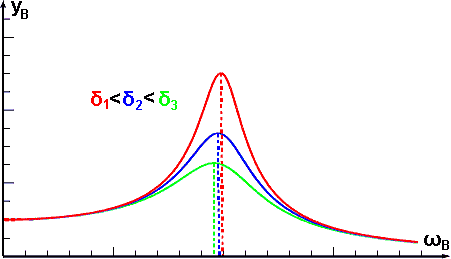
Pro poměrně značnou složitost výrazu (5) si jej vyneseme do grafu, abychom názorně viděli, jaká je závislost amplitudy yB na budící úhlové frekvenci ωB. Různé hodnoty součinitele tlumení δ budou pro nás parametrem a budou znázorňovat vliv tlumení na tvaru křivky.
Jak lze z obrázku vypozorovat, při určité budící frekvenci ωB dosahuje amplituda yB výrazného maxima. Při této frekvenci nastává jev zvaný rezonance.
Pro nalezení podmínky maxima výrazu (5) - tzv. podmínky rezonance - budeme postupovat tak, že nalezneme podmínku maxima této funkce y(ωB).
S využitím derivací dojdeme k výsledné podmínce rezonance:
Ze získaného vztahu (6) je přímo vidět, že s rostoucím součinitelem tlumení δ rezonanční frekvence postupně klesá (je vidět i v obrázku). Dosazením podmínky rezonance (6) do výrazu (5) ještě ukážeme, že s rostoucím součinitelem tlumení δ také klesá amplituda buzeného kmitání.
Interaktivní HTML5 animace:
Horní část pružiny (červené kolečko) je rozkmitávána - např. rukou - kmitavým pohybem, který považujeme za harmonický. To znamená, že je možné popisovat pohyb harmonickou funkcí (sinus nebo kosinis). Takto vzniklé oscilace oscilátoru nazýváme jako tzv. buzené kmity.
Vcelku zde můžeme pozorovat tři různé druhy chování:
Jestliže je budící frekvence velmi malá, oscilátor kmitá téměř synchronně s budícím kmitáním a i amplituda je téměř stejná.
Budící kmitání kmitá se stejnou frekvencí jako jsou vlastní kmity buzeného oscilátoru. Amplituda kmitů je silně zesílena (rezonance) a fáze buzených kmitů je o čtvrt periody posunutá vůči kmitání budícímu.
Budící frekvence je vysoká, oscilátor kmitá s velmi malou amplitudou a téměř s opačnou fází.
Jestliže je koeficient tlumení velmi malý, budou se značně projevovat přechodové stavy, proto vždy musíme nějaký čas počkat, než se v tomto případě situace ustálí a dojde k výše zmíněnému výraznému chování.
Tlačítko „Reset“ nastaví pružinu do počáteční pozice. Druhým tlačítkem můžete simulaci spustit a nebo zastavit. Zvolíte-li možnost „Zpomaleně“, zpomalí se celá simulace desetkrát. Lze též měnit základní parametry systému jako jsou tuhost pružiny, hmotnost závaží, koeficient tlumení a úhlová frekvence. Výsledky můžete zobrazovat v jednom ze tří diagramů: Závislost okamžité výchylky oscilátoru a budící síly na čase, Závislost amplitudy buzených kmitů na budící úhlové frekveci a Závislost vzájemné fáze budících a buzených kmitů v závislosti na úhlové frekvenci.