Theory
Mechanical Oscillation
Mechanical oscillations are a special case of mechanical motion of a mass point, where the point moves in a limited range around the equilibrium position. The equilibrium position is instead a stable equilibrium, which does not point to any noticeable resultant force. We choose (if possible) the center of the coordinate system to the equilibrium position. Then the position vector of a particle is equal to the deviation from the equilibrium position.
If oscillations are repeated periodically, that is, if all the physical quantities that characterize the oscillatory motion (position, velocity, acceleration) are repeated, this is a periodic and if the time course id described by sine (or cosine), also called harmonics oscillations. A system that performs mechanical oscillations is called an oscillator.
Force is the cause of all motion. The cause of oscillatory motion is the so-called directed (elastic) force. Without this force, mechanical oscillations do not exist.
We have divided oscillations by the action of forces into these basic cases:
Free oscillations occur where there is only a directing force active. (The amplitude of its free oscillation is constant, the oscillation is exactly periodic).
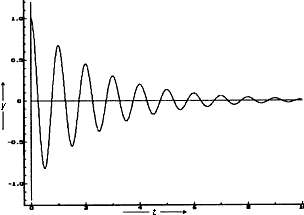
Damped oscillations occur where there is still active damping force in addition to directive forces and already no other. (Damping force can be friction, resistance of environment, etc.) Damped oscillations are almost periodic – so called quazi-periodic (amplitude decreases with time).
Forced oscillations occur where there is an external excitation force in addition to the directing and damping forces. (The amplitude of the oscillator depends on the frequency of its free oscillations and the excitation frequency.)
Free Oscillations
In the case of the spring oscillator, the guiding force is determined by the "elasticity" of the spring. This force is directly proportional to the extension of the spring, i.e. to the deflection of the oscillator. However, the direction of the force is opposite to the direction of the deflection – the spring acts against the deflection (it tries to return the system to the equilibrium position).
It can be described as:
where F – (directive) force, y – deflection of the oscillator and k – so-called stiffness of the spring (constant describing the "elasticity" of the spring).
We obtain the equation of motion (differential equation) by substituting expression (1) into Newton's second law (F = m·a). We obtain the dependence of the elongation y on the time t. This dependence has – according to the general form of harmonic motion
| where: |
ym – maximum deflection (amplitude) |
| ω – angular velocity of oscillation |
| φ0 – the initial phase of the oscillation |
the following form:
| y(t) = ym· sin( |
|
· t + φ0) |
This gives an expression for the angular frequency ω0 of the free oscillation of the equation (2) – or even better, terms for the period T and the frequency of the free oscillation f0:
Interactive HTML5 Animation:
This HTML5 application demonstrates the variation of strain, velocity, acceleration, force, and energy during the oscillation of a spring pendulum (assuming no friction).
The "Reset" button returns the pendulum body to its initial position. With the other button you can start or stop the simulation and continue it. If you select the "Slow Motion" option, the pendulum will move ten times slower. The spring constant, the mass, the gravitational acceleration and the amplitude of the oscillation can be changed within certain limits. To select a different physical quantity, click on one of the five radio buttons.
Damped Oscillations
The total energy of the oscillator decreases in real oscillators due to general losses (for example, resistance movement against environmental elements). As a result, the amplitude of the oscillations gradually decreases. In this case we speak about damped oscillations.
We can – in addition to the previously described parameters (ym, k a m) – characterize the system performing damped oscillations by the parameter δ – i.e. damping coefficient (unit s–1). This parameter describes how much the system is damped.
We can distinguish three types of motion (just by the size of damping):
1. Subcritical Damping Oscillator
If the damping of the system is relatively small (the condition δ < ω0 is fulfilled), the damping is such that it causes quasiperiodic oscillations described by the expression:
Note that not only the amplitude is changed (see below), but also the angular frequency of vibration, against undamped oscillator. We get the angular frequency of the subcritically damped oscillation ωT of the formula:
ωT = (ω02 – δ2)
In the right figure, we can see a gradual reduction in the amplitude of the damped oscillations. The amplitude has an exponentially decreasing shape in the case of subcritically damped oscillation. It also shows the expression: ym·e–δt in the expression for y(t).
2. Critically Damped Oscillator
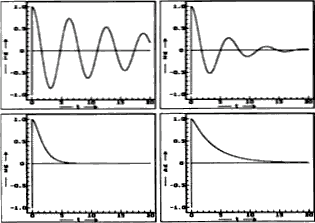
If the damping of the system is such that the condition δ = ω is satisfied, the damping of the oscillator is critical. Then it also applies that ω02 – δ2 = 0 and also ωT = 0. That is, the periodic or quasi-periodic oscillations don't occur.
We can see the waveforms of the damped oscillations for different dampings in the figure on the right. The two graphs above show the quasi-periodic oscillations with subcritical damping. (Note the different "speeds of damping" for different dampings!) At the bottom, we see a critical case (left) and supercritical damping (right). In both cases (i.e. critical and supercritical damping) we can no longer talk about oscillations.
3. Supercritical Damping Oscillator
Periodic or quazi-periodic oscillations don't occur for large damping (similar to the previous case). The condition δ > ω0 is satisfied. We then say that the damping of the oscillator is supercritical. The expression ω02 – δ2 < 0 that the angular frequency ωT doesn't exist for real numbers.
Forced (Excited) Oscillations
The total energy of the oscillator is also reduced by reducing the amplitude of subcritically damped oscillations. Thus, the oscillations disappear completely after some time. If we want to keep the oscillations, it is necessary to periodically update the lost energy by some work of external force. This is the case of an excited harmonic oscillator. The resulting oscillation is called excited or forced. Now, in addition to the directing and damping forces, the oscillator must be subjected to a periodic excitation force. The frequency of the oscillator will adapt to the frequency of the excitation force ωB after a short time. The amplitude of the oscillator, however, will depend (as we will see below) on the frequency of its free oscillations and the excitation frequency.
In general, the final excited oscillations can be described by the expression (after stabilization at the excitation frequency ωB):
where the amplitude of the resulting oscillations yB depends on the angular frequency of the free oscillation and the excited oscillation (and the damping coefficient) according to the following rather difficult expression:
| yB = |
FBm |
|
| m · (ω02 – ωB2)2 + (2 δ ωB)2 |
where FBm is the amplitude of the the excitation force, m is the mass of the weight hanging on a spring.
Resonace
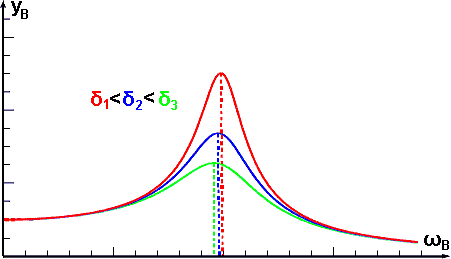
Thanks to the relatively high complexity of the expression (5) we plotted it on a graph, we see clearly what is an amplitude yB versus excitation angular frequency ωB. Different values of damping coefficient δ will be for us the parameter and it will show the damping effect on the shape of the curve.
As can be seen from the figure, the amplitude yB reaches a significant peak at a certain excitation frequency ωB. At this frequency, an effect called resonance occurs.
We'll proceed to find the maximum of the function y(ωB) in order to find the conditions of the maximum for expression (5) – the so-called resonance conditions.
Using derivation, we find the next condition
It can be seen directly from the obtained equation (6) that the resonant frequency decreases with increasing damping coefficient δ (also shown in the figure). By applying the condition of resonance (6) to expression (5), we show that the amplitude of the excited oscillations decreases with increasing damping coefficient δ.
Interactive HTML5 animation:
Interactive HTML5 animation:
The top of a spring pendulum (red circle) is moved back and forth, for example by hand; this motion is assumed to be harmonic, i.e. it can be described by a cosine function. The resulting oscillations of the pendulum are called forced oscillations.
Overall, you can see three different types of behavior:
If the frequency of the exciter is very low (i.e. the top of the spring pendulum is moved very slowly), the pendulum will oscillate almost synchronously with the exciter and with almost the same amplitude.
If the frequency of the exciter is the same as the characteristic frequency of the pendulum, the oscillations of the pendulum will build up more and more (resonance); in this case the oscillations will be delayed by about one quarter of the oscillation period compared to the exciter.
If the frequency of the exciter is very high, the resonator will oscillate with a very small amplitude and almost opposite phase.
If the damping constant (the friction) is very small, the transient states will also be important; therefore, in this case, you will have to wait some time to notice the mentioned types of behavior.
The "Reset" button returns the pendulum to its initial position. The other button allows you to start, stop and continue the simulation. If you select the "Slow Motion" option, the pendulum will move ten times slower. The spring constant, the mass, the damping constant and the angular frequency of the excitation oscillation can be changed within certain limits. In addition, you can select one of three diagrams using the corresponding radio buttons: The expansions of the exciter and the resonator as a function of time, The amplitude of the resonator oscillation as a function of the angular frequency of the exciter, and The phase difference between the oscillations of the exciter and the resonator as a function of the angular frequency of the exciter.